First-order wave motions due to the presence of Regular Airy Waves are computed as follows:
![]() (1)
(1)
where:
•di(t) is the instantaneous displacement in a particular degree of freedom, i (heave, surge, sway, yaw, roll or pitch)
•t is the instantaneous solution time in seconds
•N is the number of regular Airy waves
•RAOi(θ,ω) is the RAO magnitude in degree of freedom i, which is a function of Incident Wave Heading θ and wave frequency ω
•an is the amplitude of the nth regular wave (MWL to crest or trough)
•kn is the wave number of the nth regular wave (k = 2π/λ, where λ is wavelength)
•sn is the horizontal distance from the global X axis to the vessel reference point in the direction of wave propagation for the nth regular wave (sn = y cosθn + z sinθn, where y and z are the instantaneous coordinates of the vessel reference point in the global Y and Z axes respectively)
•ωn is the circular frequency of the nth regular wave
•φn is the phase of the nth regular wave relative to zero datum
•Φi(θ,ω) is the RAO phase angle in degree of freedom i, which is a function of wave heading θ and wave frequency ω. Note that a positive phase angle denotes a phase lag relative to the incident wave harmonic at the vessel reference point.
If there is only a single regular Airy wave present, then the summation from 1 to N in Equation 1 is obviously not required.
All random seas (including Pierson-Moskowitz, Jonswap, Ochi-Hubble, Torsethaugen and User-defined) are simulated using a series of individual component harmonics which are generated using a Spectrum Discretisation technique. Each harmonic is basically a regular Airy wave, so Equation 1 above remains valid.
A slightly different modelling procedure is used for Stokes V and Dean’s Stream waves. You should refer to the relevant articles for further information, where the computation of vessel response is discussed for each of the various response settings.
The handling of first order or high frequency motions calculated via RAOs is slightly different from the handling of drift motions described earlier. This is because the derivation of RAOs is such that they do genuinely represent motions in vessel degrees of freedom (heave, surge, sway, yaw, roll, and pitch).
So dealing first with translations, the three values calculated by Flexcom define heave, surge and sway relative to the instantaneous yawed vessel axis system of the Instantaneous Vessel Axes – Large Angles figure. So heave represents motion in the global X direction. Surge is directed along an axis in the global YZ plane which is the global Y axis rotated through {θ + Ψ + γD(t)} about global X. The sway axis is likewise the global Z axis rotated through the same angle.
The three RAO rotations likewise represent yaw, roll and pitch relative to the yawed axis in the Instantaneous Vessel Axes – Large Angles figure. These define the components of a rotation vector in the terminology of the Flexcom kinematics algorithm, and are combined with rotations due to static offset and drift using standard Flexcom techniques.
At a given instant in time, Flexcom calculates the amplitudes of the individual rotations from the wave amplitude and the vessel RAOs. So for example, the amplitude of the yaw response (Ayaw) is equal to the wave amplitude times the yaw RAO. The magnitudes of the roll (Aroll) and pitch (Apitch) responses are computed in a similar manner. Based on Ayaw, Aroll and Apitch, a single ‘unit rotation vector’ is established about which a single rotation takes place. The magnitude of this rotation is:
![]() (2)
(2)
The unit vector about which this rotation takes place is defined by the following x, y and z components in the vessel axis system:
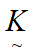 (3)
(3)
The sense of the rotation follows the right hand rule. Specifically, when looking along the unit vector (from the origin, looking along the unit vector) the sense of the rotation is clockwise. For illustration purposes, supposing the individual yaw, roll and pitch terms are all equal to 69.28°, then this would represent an overall rotation of 120° about the vector {0.577, 0.577, 0.577}, rotating clockwise, from the perspective of a viewpoint located at the origin and a direction aligned with the vector.
Of course in an analysis with no low frequency drift motions, the RAO motions are relative to the axis system produced by the vessel static offset, which is shown in the Vessel Axes following Yaw Offset – Large Angles figure. Likewise if there is no offset or drift, RAO motions are defined in terms of the undisplaced axis system of the Initial Orientation of Vessel Axes figure.
Finally, in an analysis where RAOs are specified as a function of wave heading, wave headings at any time are calculated relative to the instantaneous orientation of the vessel axes as shown in the Instantaneous Vessel Axes – Large Angles figure. The calculation of wave heading does not take into account the changing orientation of the axes due to first order yaw. In an analysis with no drift, wave headings are invariant with time, and are calculated with respect to the yawed axes of the Vessel Axes following Yaw Offset – Large Angles figure. If there is neither offset nor drift, then the invariant headings are calculated with respect to the undisplaced axes of the Initial Orientation of Vessel Axes figure.
The three translations calculated from vessel RAOs by Flexcom define heave, surge and sway relative to the undisplaced vessel axes of the Instantaneous Vessel Axes – Large Angles figure in the small angle case.
The three RAO rotations likewise represent yaw, roll and pitch relative to the undisplaced vessel axes. Once again they are combined with offset and drift rotations by summing separately the contributions due to each of yaw, roll and pitch. Finally, where vessel RAOs are specified as a function of wave heading, the heading is calculated relative to the undisplaced vessel axes.
•*VESSEL,INTEGRATED is used to specify all information pertaining to a vessel or vessels. Specifically, the ANGLES= input is used to specify the theory used to combine vessel rotations.
•*VESSEL is used to specify the initial position and undisplaced orientation of a vessel.
•*RAO is used to specify Response Amplitude Operators for a vessel.
Note also that the old *VESSEL and *RAO keywords have effectively been superseded by the new *VESSEL,INTEGRATED keyword, which accepts RAO data also, thereby eliminating the need for a separate *RAO keyword – hence the ‘integrated’ nature of the new keyword.