Non-Linear Power-Law Connections |
 
|
Non-Linear Power-Law Connections |
|
Non-linear connections, whether standard or sliding, can now be defined using a power-law approach, defined in terms of a maximum contact force and an exponential coefficient (the latter parameter is optional and defaults to a value of 10 if omitted). Earlier versions of Flexcom required that you explicitly defined non-linear connections as force-deflection pairs, and while this approach is still retained for complete generality, the power-law approach is more convenient, requiring far less input on the part of the user.
•The user does not have to manually define a force-deflection relationship in terms of explicit data points
•It ensures a gradual transition between regions of low and high stiffness, which aids solution robustness
•It ensures that the slope of the force-deflection relationship is monotonically increasing with increasing displacement, which again aids solution robustness, particularly given that the pipe-in-pipe contact is based on the Tangent Stiffness method.
•For cases of Sliding Connections, for example a J-Tube Pull-In, the force-deflection relationship is automatically updated during a simulation to reflect contact diameters of connected elements at different points in time
For pipe-in-pipe type configurations, Flexcom automatically generates a non-linear relationship of the form:
where:
•
is the instantaneous resistive force in the lateral direction provided by the connection
•
is the user-specified maximum contact force
•
is the relative displacement of the connected nodes in the lateral direction
•
is the maximum displacement of the connected nodes in the lateral direction before the inner and outer pipes come into contact. Specifically, 
, where 
is the internal diameter of the outer pipe, and 
is the external (contact) diameter of the inner pipe.
•The 
parameter is automatically computed by Flexcom based on the instantaneous diameters at any point in time. This means that the non-linear relationship remains accurate at all times, even for sliding connections where the relevant diameters may vary as the pipes move in the axial direction.
•
is the user-specified exponent
For pipe-on-pipe type configurations, Flexcom automatically generates a non-linear relationship of the form:
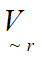
where:
•
is the instantaneous resistive force in the lateral direction provided by the connection
•
is the user-specified maximum contact force
•
is the initial separation between the connected nodes in the lateral direction, taking external (contact) diameters into account
•
is the instantaneous separation between the connected nodes in the lateral direction, taking external (contact) diameters into account
•
is the user-specified exponent
Note that, given the above definitions, non-linear connections defined using a power-law approach are only meaningful for modelling resistance for pipe-in/on-pipe connections in the lateral direction. The option should not be used for modelling axial resistance.
Flexcom users regularly seek guidance regarding suitable values of both the maximum contact force and exponent entries. It is difficult to provide a definitive answer to this question as the optimal parameters may vary between different models. However, the following guidelines should be helpful.
•Using a high exponent value will align the analytical and theoretical solutions. However, the rationale behind the exponent input is that it allows the user to control the application of the contact stiffness term. Very high exponents can lead to solution convergence issues, as the contact stiffness can vary significantly over extremely small ranges of displacement. It could also cause an increase in run-time, as more solution iterations may be required to achieve convergence at every solution time step. Using an exponent term affords a reasonable compromise between theoretical accuracy and solution efficiency/robustness.
•In order to facilitate inspection of the automatically generated power-law relationship, the Flexcom output file presents a table illustrating the variation in contact force with lateral displacement, in both percentage and absolute terms. If you would like to visually check the force-deflection relationship for different values of exponent, this table may be easily imported into a spreadsheet and plotted graphically.
•The maximum contact force needs to be sufficiently high to prevent any significant penetration between the pipes (which would represent a physically unreasonable configuration). What constitutes an acceptable level of penetration is very much a subjective decision on the part of the user. Remember that the exponent value tends to compensate against any penetration also, so both inputs are interdependent to some degree. Rigid pipes may require a higher contact force than more flexible ones.
•From an engineering perspective, any possible misinterpretation of results would represent a more important concern than a slight compromise of modelling accuracy (e.g. in an effort to aid solution robustness). This point merits further elaboration.
oMinor adjustments to the maximum force and exponent inputs may not make any significant difference in the context of a global analysis. For example, the overall model configuration should look largely similar, regardless of these specific inputs. Assuming the overall displacements are consistent with expectations, then parameters like bending moment and curvature should be reasonably accurate also. In summary, using moderate, rather than extreme, values of maximum force and exponent should not lead to any appreciable loss in precision.
oIf the solution exhibits high frequency noise, this is most likely a numerical issue which does not represent a physical phenomenon. Unexpected peaks in bending moment for example, may be induced by using excessively large maximum force and/or exponent terms. Many users employ Summary Postprocessing and Collation, and some users may rarely examine individual time history plots. Spurious peaks, going unnoticed, could conceivably distort the overall structural design. In summary, it is preferable to accept a slight modelling compromise, rather than striving for theoretical accuracy, which may come at the expense of introducing uncertainties.
•If you are concerned about optimal values of maximum force and/or exponent, performing some sensitivity studies may provide greater insight. For example, you could examine the effect of varying these parameters on bending moment in the connected pipes. Considering just one dynamic load case should serve as a useful starting point. This approach could also provide a validation of the advice presented in the previous point.
Based on the experience of the Flexcom technical support team, the following rules of thumb may be useful.
•A maximum contact force of 1.0E+06 N is recommended. Using higher values have been shown to contribute to numerical noise.
•An exponent value of between 10 (lower bound) and 50 (upper bound) is recommended.
Switching on node numbers in the Model View will allow you to identify Contact Nodes. Once the separation between the connected nodes (as per the definitions above) has reduced to 10% of its initial value (i.e. 90% gap closure), both nodes in the contact pair are highlighted.
•*PIP CONNECTION is used to define pipe-in-pipe connections between nodes of the finite element model.
•*PIP STIFFNESS is used to define force-deflection curves for non-linear pipe-in-pipe connection stiffnesses. Specifically, the TYPE=POWER LAW input is used to create a non-linear contact relationship based on a power law approach.
If you would like to see an example of how these keywords are used in practice, refer to H02 - J-Tube Pull-In.