The pipe-in-pipe contact modelling algorithm performs a number of sequential stages. These same stages are applied to every pipe-in-pipe connection, at every solution iteration. The only exception being Inactive Connections - these are sliding connections which are deemed to have become inactive following excessive relative axial motion between the connected pipes.
Firstly, the relevant finite element nodes in the pipe-in-pipe connection are identified. For standard connections, the primary and secondary nodes are defined during model set-up, and remain the same throughout the analysis. For sliding connections, each connection is defined by a primary node which remains consistent, and a secondary node whose identity may vary from one solution time step to the next.
A primary element is also identified for each pipe-in-pipe connection. Identification of the primary elements is important, as the local contact stiffness terms are applied in a direction which is perpendicular to each primary element. The primary element must contain the primary node as one of its end nodes. Where a contact node is shared between two or more elements, the first (lowest numbered) element is selected.
For top tensioned risers which are numbered from bottom to top, the primary elements typically lie immediately underneath the primary nodes. In such circumstances, structural curvatures generally vary little from element to element, so the distinction between a primary element which is just above or just below the connected nodes is immaterial. However, you are naturally free to alter the model set-up (which is very easy if the model is built using Lines) should you wish to influence the selection of the primary element.
Next a 3x3 transformation matrix is assembled for the pipe-in-pipe connection. Its purpose is to facilitate transformation of information between the local axis system associated with the pipe-in-pipe connection, and the global axis system in which Flexcom computes its solution. Each row of the matrix corresponds to a local vector, local-x, local-y and local-z.
The local-x vector corresponds to the instantaneous (convected) local-x axis of the Primary Element. Specifically the local-x vector points directly between the start node and the end node of the primary element. If the element length is zero for some reason (this would be expected for Hinge Elements, and theoretically possible for beam or spring elements experiencing severe compressive strain), then the local-x vector is assumed to be aligned with the global-X vector. Finally the local-x vector is normalised.
The local-y vector is defined in a plane which is perpendicular to the local-x vector. A simple procedure is used as follows. If the first component of the local-x vector (x1) is non-zero, then the local-y vector is defined as {-x2/x1,1,0}. Otherwise, if the second component of the local-x vector (x2) is non-zero, then the local-y vector is defined as {0,-x3/x2,1}. Otherwise, the local-y vector is defined as {1,0,-x1/x3}. Finally the local-y vector is normalised. Although the procedure may seem somewhat arbitrary, the only important aspect at this stage is the orthogonality of the local-x and local-y vectors.
The local-z vector is formed from the cross product of the local-x and local-y vectors. The 3 local vectors are then inserted into the 3 rows of the (global to local) transformation matrix. An inverse matrix is also created to facilitate reverse operations, from local to global.
A new vector is now assembled which points directly between the instantaneous positions of the primary and secondary nodes of the pipe-in-pipe connection. This vector is then transformed from the global to local axis system using the assembled transformation matrix. The axial component of this local vector is then suppressed by setting the local-x term to zero, which equates to a projection of the vector onto the local y-z plane. This vector is then transformed back into the global axis system, where it effectively represents a vector which is (i) perpendicular to the primary element and (ii) lies in a plane which contains both the primary and secondary nodes of the pipe-in-pipe connection.
By default, the connection vector is calculated on the basis of the instantaneous structure configuration. It is possible to instruct Flexcom to base the connection vector on the initial structure configuration (via the ORIENTATION=INITIAL option under the *PIP CONNECTION keyword), and this may help solution stability in exceptional circumstances. For example, if the lateral movement of the inner pipe with respect to the outer pipe is small in magnitude but variable in direction, this can cause the instantaneous orientation of the connection vector to continually change between successive solution times. However this is very much the exception, and the default operation is the preferred and recommended method for the majority of models.
Now a newer, more refined transformation matrix is assembled for the pipe-in-pipe connection. This matrix is central to the integration of the pipe-in-pipe module into the global solution. It has 3 components, each of which corresponds directly to one of the local degrees of freedom of the pipe-in-pipe connection. Hence the terms longitudinal, normal and transverse are used from this point onwards, rather than generic terms such as local-x, local-y and local-z.
•The longitudinal axis of the local axis system corresponds to the instantaneous (convected) local-x axis of the primary element, as discussed in the Transformation Matrix section.
•The normal axis of the local axis system is perpendicular to the local-x vector, and lies in a plane which contains both the primary and secondary nodes, as discussed in the Connection Vector section.
•The transverse axis of the local axis system completes the right handed system.
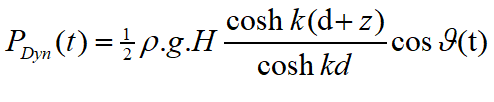
An inverse transformation matrix is also created to facilitate reverse operations.
For pipe-in-pipe connections which have been assigned a linear connection stiffness, the relevant stiffness term is quickly identified from the relevant keyword entry (i.e. the numerical value specified following the STIFFNESS= option under the *PIP CONNECTION keyword).
For pipe-in-pipe connections which have been assigned a non-linear connection stiffness (using the CURVE= option under the *PIP CONNECTION keyword, and the *PIP STIFFNESS keyword), the procedure is slightly more involved. Firstly, the relative displacement of the primary and secondary nodes is computed based on the instantaneous positions of these nodes with respect to their initial positions. Displacements are solved in the global axis system, so the relative displacement vector is computed in a global context, and then transformed into the local axis system using the pre-defined Transformation Matrix. The normal component of this vector, representing the relative displacement of the connected nodes in the lateral direction, is then used in conjunction with the relevant non-linear force-deflection curve to determine the instantaneous contact stiffness.
If the non-linear force-deflection curve has been defined using explicit Data Pairs, Flexcom loops through the deflection values searching for two consecutive values which lie either side of the lateral displacement term. Linear interpolation is used to determine the relevant stiffness of the connection. If the lateral displacement term lies outside the specified range of the force-deflection values, extrapolation is used, based on the force-deflection terms at the lower or upper extremity as appropriate.
If the non-linear force-deflection curve has been defined using the Power-Law approach, the instantaneous stiffness is readily derived from the power-law equation.
•For pipe-in-pipe models (i.e. *PIP STIFFNESS -> TYPE=POWER LAW -> CONFIGURATION=PIP), the maximum lateral displacement is defined as...
![]()
where ![]() is the internal diameter of the outer pipe, and
is the internal diameter of the outer pipe, and ![]() is the external (contact) diameter of the inner pipe.
is the external (contact) diameter of the inner pipe.
•The lateral displacement term is expressed as a percentage of maximum displacement. Where relative penetration has occurred (percentages greater than 100%), the percentage value is reset to the maximum value of 100%. This prevents the numerical model from creating contact forces which are greater than the user specified Maximum Contact Force. A pair of force-deflection values is computed in the region of the percentage value, corresponding to the nearest integer percentage values. For example, if the instantaneous lateral displacement is 82.4% of the maximum displacement value, then actual deflection values are defined at 82% and 83% of maximum displacement. Corresponding force values are then computed using the Pipe-in-Pipe Power-Law equation. Linear interpolation is used to determine the instantaneous stiffness of the connection. Note that pipe-in-pipe contact is based on the Tangent Stiffness method.
•For pipe-on-pipe models (i.e. *PIP STIFFNESS -> TYPE=POWER LAW -> CONFIGURATION=POP), the maximum lateral displacement is defined as the initial separation between the connected nodes in the lateral direction, taking external (contact) diameters into account. Again the lateral displacement term is expressed as a percentage of maximum displacement. Thereafter the procedure is very similar to that just described for the pipe-in-pipe case, except that the Pipe-on-Pipe Power-Law equation is used instead.
Consistent with the Local Axis System discussion, the contact stiffness as just described is denoted the normal stiffness, Kn.
It is not currently possible to model the effects of axial friction between sliding pipes. However some degree of resistance to relative axial motion may be simulated using the axial stiffness inputs. Linear axial stiffness values may be specified via *PIP CONNECTION -> AXIAL_STIFF, while non-linear axial force-deflection relationships may be specified via *PIP CONNECTION -> AXIAL_NONLINEAR.
For pipe-in-pipe connections which have been assigned a linear axial stiffness, the relevant stiffness term is quickly identified from the relevant keyword entry.
For pipe-in-pipe connections which have been assigned a non-linear axial stiffness, the procedure is slightly more involved, but is conceptually similar to that discussed in the Contact Stiffness section. Firstly, the relative displacement of the primary and secondary nodes is computed based on the instantaneous positions of these nodes with respect to their initial positions. Displacements are solved in the global axis system, so the relative displacement vector is computed in a global context, and then transformed into the local axis system using the pre-defined Transformation Matrix. The axial component of this vector, representing the relative displacement of the connected nodes in the axial direction, is then used in conjunction with the relevant non-linear force-deflection curve to determine the instantaneous axial stiffness. The linear interpolation technique used is identical to that discussed previously.
Consistent with the Local Axis System discussion, the axial stiffness is denoted the longitudinal stiffness, Kl.
The governing entries are naturally the lateral and axial stiffness discussed in the previous sections. There is one further term, called the transverse stiffness, Kt. For reasons of numerical stability, and to a lesser extent to represent a physical resistance to transverse motion when two pipes have come into contact in a normal direction, a transverse stiffness term is computed and inserted at 90° to the normal stiffness term.
For pipe-in-pipe connections which have been assigned a linear connection stiffness, the same stiffness term is used in both lateral degrees of freedom. Specifically, Kt = Kn.
For pipe-in-pipe connections which have been assigned a non-linear connection stiffness, the transverse stiffness depends on the instantaneous configuration. If the connected nodes experience some degree of physical separation in the lateral plane, the Local Axis System will have already been determined with absolute certainty. In this case, the same stiffness term is used in both lateral degrees of freedom. Specifically, Kt = Kn. If the connected nodes are perfectly coincident, which might be the case for concentric pipe sections prior to the application of any external loading, the local axis system may be somewhat arbitrary. In this case, the transverse and normal directions are treated independently, and the transverse stiffness is computed using the procedure already documented in the Contact Stiffness section.
A local 12x12 stiffness matrix is assembled for the pipe-in-pipe connection. Flexcom actually uses a fourteen degree of freedom Hybrid Beam Element, where the axial force and torque are added to the usual form of a three-dimensional beam element. However these additional degrees of freedom are not relevant to pipe-in-pipe connections.
The local stiffness matrix is populated as follows.
Local Stiffness Matrix
The local stiffness matrix is then transformed into the global axis system, using a 12x12 version of the (inverse) Transformation Matrix defined earlier. This is then used to augment the global finite element stiffness matrix at the appropriate locations.
All of the terms discussed up to this point relate to the stiffness matrix which appears on the left hand side of the Finite Element Equations of Motion. Some additional terms also need to be assembled and inserted into the global force vector on the right hand side.
There are two separate items which fall into this category, stemming from rigid body motions, and non-linear pipe-in-pipe connections.
•Because Flexcom solves for position rather than displacement, forces corresponding to rigid body motions must be included in the global force vector. This approach applies to all elements in the Flexcom solution, but the steps relevant to pipe-in-pipe connections are outlined here. The initial separation between the connected nodes is assembled into a local vector, with longitudinal, normal and transverse (zero by definition) terms, consistent with the definition of the Local Axis System outlined earlier. This initial separation vector is then transformed into the global axis system using the inverse Transformation Matrix, where it is then added into a 12x1 column vector at appropriate locations. This displacement vector is then multiplied by the global stiffness matrix for the pipe-in-pipe connection to produce the relevant right hand side force vector. This is then used to augment the global force vector at the appropriate locations.
•Although not explicitly mentioned in the preceding sections on Contact Stiffness and Axial Stiffness, a force term is also computed and stored during the same operation which returns the instantaneous stiffness of non-linear connections. As noted earlier, the stiffness term is equal to the tangent slope of the force-deflection relationship at the relevant displacement. The force term is the point on the force axis where the tangent slope intersects it. This is conceptually similar to the Non-linear Material Force Term associated with non-linear materials. The force terms are used to populate a 12x1 column vector at appropriate locations. Assuming the normal and transverse force terms are identical, the local force vector would be assembled as follows.
![]()
Local Force Vector
The local force vector is then transformed into the global axis system, using a 12x12 version of the (inverse) Transformation Matrix defined earlier. This is then used to augment the global force vector at the appropriate locations.