This section presents the finite element equations of motion, based on equating internal and external virtual work expressions.
By substituting for the stress and strain expressions in the virtual work statement given by Internal Virtual Work Statement (Eq.11), and equating internal and external work increments given by Internal Virtual Work Statement (Eq.11) and External Virtual Work Statement (Eq.2), the local form of the equations of motion are derived as:
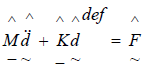 (1)
(1)
The local hybrid stiffness matrix is decomposed to:
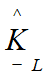 (2)
(2)
where ![]() is the standard beam-column linear stiffness matrix, and
is the standard beam-column linear stiffness matrix, and ![]() and
and ![]() are given by:
are given by:
and:
where:
![]() (5)
(5)
![]() and
and ![]() are respectively the initial displacement matrix and the geometric stiffness matrix. Equation (1) above can now be transformed from the local convected to the global axes resulting in the equation:
are respectively the initial displacement matrix and the geometric stiffness matrix. Equation (1) above can now be transformed from the local convected to the global axes resulting in the equation:
where:
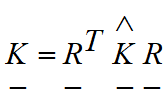 (7)
(7)
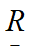 (8)
(8)
 (9)
(9)
and ![]() is the transformation matrix from local to global axes.
is the transformation matrix from local to global axes.