Internal Virtual Work Statement |
 
|
Internal Virtual Work Statement |
|
The generalised stress field 
for a three dimensional beam, as illustrated in the Convected Axis System, is given by:
where:
•
is axial force, and
•
are the moments about the three axes
Since it is intended to apply penalties to the axial force and torque moment quantities using Lagrange constraints, an additional vector 
is defined as:
(2)
where 
and 
are independent variables and are solved for directly in the set of finite element equations.
The generalised strains 
conjugate to the stresses in the above Equation are written in terms of linear and nonlinear components as follows:
(3)
Here:
(4)
and:
(5)
A prime denotes differentiation with respect to the coordinate 
along the local convected beam axis shown in the Convected Axis System. The nonlinear strains in the equation directly above indicate that moderate rotations with respect to the convected axes are included. They may be expressed more conveniently in the form:
where:
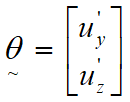(7)
and:
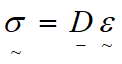(8)
Finally, the stress-strain relationship is written simply as:
(9)
where 
is an elastic constitutive matrix constructed as:
The internal incremental virtual work statement for this hybrid formulation is now expressed as:
where:
•
is an increment of internal virtual work
•L is the length of the beam element
•
is the identity matrix
and:
(12)
The matrix 
is a weighting matrix, and the values of 
and 
depend on the flexibilities of particular elements. The third integral in the above equation is the Lagrangian constraint imposing the penalty terms on the axial force and torque variables.
