Finite Element Model |
 
|
Finite Element Model |
|
The local displacement vector relative to the convected axes 
for a point on the pipe element shown in the Convected Axis System is defined as:
(1)
Similarly, the local rotation vector 
is given as:
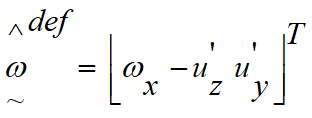(2)
Since the rotations are assumed small relative to the convected axes, the above equation may be written as:
(3)
The total local nodal solution vector 
for the two-noded pipe element may be written as:
(4)
The standard twelve degrees of freedom are augmented in this case by the independent axial force and torque variables.
The vector of the solution variables at any point on the pipe element 
is found by interpolating the nodal vector as follows:
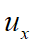(5)
where linear interpolation is used for the axial components 
and 
; cubic functions for the transverse displacements 
and 
; and the generalised forces 
and 
are assumed constant over the element. The rotations 
and 
may also be expressed in terms of the nodal vector where:
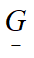(6)
Clearly, 
is obtained directly from the functions given by 
. Similarly, the penalty terms may be written as:
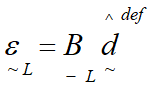(7)