Finite Rotation Kinematics |
 
|
Finite Rotation Kinematics |
|
The coefficient vector associated with the stiffness matrix in the Equations of Motion (Eq.6) is written in terms of the deformations with respect to the convected axes. In order to use this equation to solve the complete system, Equations of Motion (Eq.6) must be expressed in terms of the total nodal solution vector 
. With reference to the figure below, the translation deformation components of a material point on a pipeline may be written as:
(1)
where 
is the rigid body translation vector of a material point on the convected axes.
Translation of Material Point
However, the same simple decomposition cannot be applied to the finite rotational components since they do not behave as vectors.
The finite rotation of a material point on the pipeline may be represented by the line segment 
, whose magnitude is the amount of the rotation and whose direction is the axis about which the rotation occurs and is in the sense defined by the right-hand rule. The line segment 
is not a true vector since addition is not commutative. A finite rotation can also be represented by an orthogonal matrix 
whose components are uniquely determined by the components of 
. We can incorporate the rigid body rotation of the convected axes from the undeformed pipe orientation by the equation:
(2)
where 
corresponds to the rigid body rotation 
of the convected axes, and 
corresponds to the rotation 
of the material point from the convected axes.
Now consider two material points on the beam a and b at a distance 
apart, and write that:
(3)
where 
corresponds to a rotation 
, 
corresponds to a rotation 
, and 
corresponds to an incremental rotation 
. Note that 
is not the algebraic difference between 
and 
, but must be found from Equation (3). A rate of rotation vector 
may now be defined as:
(4)
and is a true vector quantity in the limit of small rotations.
An examination of Equations (3) and (4) reveals that the definition of the rate of rotation is independent of the reference configuration from which the rotation is measured. Therefore it is possible to define two vector quantities 
and 
such that:
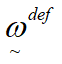(5)
Additionally, rotations 
relative to the convected axes are small by definition and so behave as true vectors; therefore it is possible to define 
as:
(6)
Integrating Equation (5) and incorporating Equation (6) yields
(7)
where 
is a constant vector determined from the integration of Equation (5) and associated with the rigid body rotation of the convected axes.
Note that 
and 
are true vectors, but are not the same as the actual rotations 
and 
, respectively. However, Equation (7) shows that by using the so-called quasi-rotation vector 
it is possible to isolate a rigid body term 
associated with the rigid body rotation of the convected axes. The decomposition represented by Equation (7) is also of the same vector form as Equation (1).
If the quantities in Equation (7) are re-interpreted as nodal rotational components, the following decomposition is possible for the total nodal vector:
(8)
For completeness, the terms in 
are listed as:
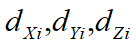(9)
where:
•
are the components in global axes of displacement of Node i from undeformed position
•
are the components in global axes of quasi-rotation vector at Node i
Substituting Equation (8) into Equation (5), the final form of the finite element equations of motion is obtained as:
(10)
Stiffness and mass proportional damping terms may also be included in the equations of motion, in which case Equation (10) is modified to become:
(11)
where 
and 
are damping coefficients and 
is the vector of nodal velocities. The equation for a pure static analysis is given by:
(12)
where the load vector 
in this case contains static loading only.