Hydrodynamic Loading |
 
|
Hydrodynamic Loading |
|
Hydrodynamic forces calculated from Morison’s Equation act in general in three dimensions on a structure. The forces combine drag and inertia/added mass components. The drag force at a point on an element is written in terms of the relative fluid/structure velocity 
at that point, which is given by
(1)
where:
•
is the water particle velocity due to wave action
•
is the current velocity from user-specified constant (time-invariant) current distribution
•
is the velocity specified via a current user subroutine
•
is the structure velocity
Dealing first with 
in the case of a regular wave analysis this term is calculated using standard Airy, Stokes V or Dean’s Stream Function wave theory, depending on user specification. In the case of a random sea analysis, such as a Pierson-Moskowitz, Jonswap, Ochi-Hubble or Torsethaugen wave spectrum, 
is a summation of terms, specifically:
(2)
where:
•
is the water particle velocity due to ith wave harmonic
•
is the number of harmonics into which the wave spectrum is discretised
The spectrum discretisation algorithms are discussed in Spectrum Discretisation. 
for each harmonic is calculated using standard linear Airy wave theory, since Stokes or Dean’s Stream Function waves cannot be superposed.
The term 
is strictly speaking unknown at each solution time. Flexcom uses the structure velocity from the previous iteration in calculating 
. At the first iteration at a particular solution time, the velocity from the previous solution time is used.
has components normal and tangential to the element in the convected axes. These are denoted by 
and 
respectively, and are given by
(3)
and
(4)
where:
•
is the unit vector in the element axial direction of the convected axes.
For the inertia/added mass components, expressions are required for water particle and structure acceleration components in the local axes for the Morison’s Equation hydrodynamic force. The total water particle acceleration vector in global axes 
is defined as
(5)
where:
•
is the water particle acceleration due to wave action
•
is the acceleration specified via current user subroutine
is calculated from Airy, Stokes V or Dean’s Stream Function wave theory in the case of a regular wave, and from a summation of Airy wave terms in the case of a random sea.
The structure acceleration vector in global axes is denoted 
. Like 
, 
is unknown at each solution time, but the acceleration term is handled differently to the velocity term, as discussed further below. To calculate hydrodynamic forces, both 
and 
are finally resolved into components normal and tangential to the convected axes, using analogous expressions to the two Equations above.
The components of the hydrodynamic force in the normal and tangential directions, denoted 
and 
respectively, are now defined as
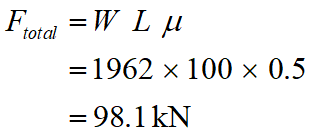(6)
and
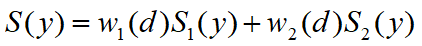(7)
where:
•
is the drag diameter of the element
•
is the drag (
) or buoyancy (
) diameter, depending on user specification
•
is the drag coefficient in direction normal to element
•
is the inertia coefficient in direction normal to element
•
is the added mass coefficient in direction normal to element
▪This defaults to 
unless specified otherwise
•
is the component of 
normal to element
•
is the component of 
normal to element
•
is the drag coefficient in direction tangential to element
•
is the added mass coefficient in direction tangential to element
•
is the inertia coefficient in direction tangential to element
▪note that this term is not a user input – it is assumed to be equal to 
•
is the component of 
tangential to element
•
is the component of 
tangential to element.
The last term in both of these equations is proportional to a component of the structure acceleration 
. These terms are not actually integrated into the right-hand side force vector. Instead they are taken to the left-hand side of the equations of motion and integrated into the element mass matrix.
Traditionally, Flexcom has based the calculation of both the drag and the inertia/added mass components of Morison’s Equation on the drag diameter. This is retained as the default operation to maintain compatibility with older program versions. However, strictly speaking the added mass and inertia terms should be based on displaced volume (defined by the buoyancy diameter) as opposed to projected area (defined by the drag diameter), and an option is now provided to select this approach.
Note that the application of drag and hydrodynamic inertia loads for inner pipe-in-pipe elements requires that pipe-in-pipe connections exist between the inner and outer pipe-in-pipe nodes. Please refer to the Hydrodynamic Forces section for more information on this.
•*HYDRODYNAMIC SETS is used to assign hydrodynamic coefficients to element sets.
•*CURRENT is used to specify current loading.
•*WAVE-REGULAR is used to specify regular Airy wave loading.
•*WAVE-STOKES is used to specify Stokes V regular wave loading.
•*WAVE-DEANS is used to specify Dean’s Stream regular wave loading.
•*WAVE-PIERSON-MOSKOWITZ is used to specify a Pierson-Moskowitz random sea wave spectrum or spectra.
•*WAVE-JONSWAP is used to specify a JONSWAP random sea wave spectrum or spectra.
•*WAVE-OCHI-HUBBLE is used to specify an Ochi-Hubble random sea wave spectrum or spectra.
•*WAVE-TORSETHAUGEN is used to specify a Torsethaugen random sea wave spectrum or spectra.
•*WAVE-TIME-HISTORY is used to specify a random seastate in terms of a time history of water surface elevation.
•*WAVE-USER-DEFINED is used to specify a User-Defined random sea wave spectrum or spectra.