Drag Linearisation |
 
|
Drag Linearisation |
|
The hydrodynamic forces on an offshore structure are calculated using the standard Morison’s Equation formulation. The forces predicted using this approach include drag and inertia components. The inertia component is linear and does not present any difficulty with respect to the application of Dynamic Solution (Eq.5). However the drag component is quadratic, and this component must be replaced by an equivalent linear term chosen on the basis of a best fit between linear and non-linear forms, if the above frequency domain development is to remain valid. The development of this best fit linearisation is summarised here. It is not however proposed to present detailed mathematics - interested readers are referred to relevant publications for detailed presentations. A more detailed version of the material presented in this section is described by McNamara. & Lane (1991). The program regular wave drag linearisation is based on the procedure described by Hamilton (1980). The program random sea drag linearisation follows the method of Langley (1984).
The formulation of the hydrodynamic drag via Morison's equation is based on the relative fluid/structure velocity vector 
at any point on the structure, which is given by:
(1)
Here 
is water particle velocity due to waves, 
is structure velocity and 
is current velocity. All of these vectors are expressed in global coordinate axes. Morison's equation forces are more meaningfully calculated in a local axis system with components normal and tangential to an arbitrarily inclined element. We transform 
into 
in this local system (the subscript ^ denoting local axes), with components:
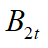(2)
where 
and 
indicate vectors tangential and normal to an element, and 
is a unit vector in the tangential direction.
Tangential and normal pressure vectors due to fluid drag are now defined using Morison's equation as follows:
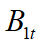(3)
where 
is water density, 
is drag diameter, and 
and 
are respectively tangential and normal drag coefficients.
The development of the form of the full non-linear drag involves writing expressions for 
and 
similar to Dynamic Soluation (Eq.1) and Dynamic Solution (Eq.5). From these, expressions for 
, 
and ultimately 
can be found. However the form of 
in the Equation above makes it clear that Dynamic Solution (Eq.5) will not be valid.
Drag linearisation involves replacing the quadratic forms in Equation (3) above by equivalent linearised terms chosen to minimise the error between linear and nonlinear forms. The linearised pressure vector can be written as:
(4)
Here the velocity terms due to waves and current (
and 
respectively) and the structure velocity 
have been rotated to local axes and resolved into tangential and normal components. The 
terms are the linearisation coefficients, which take various forms for wave loading with and without current, and for regular waves or random seas. Note that the tangential linearisation coefficients and are scalars, since the tangential drag is independent of the normal components and is effectively one-dimensional. For the normal direction on the other hand the linearisation coefficients 
and 
are matrices.
There are two important points to note about Equation (4) above. Firstly, it does permit the decomposition of drag forces into time-varying and time-independent components as required by Mathematical Background (Eq.3). Secondly, it does also allow the time-varying drag force to be expressed in the form of Dynamic Soluation (Eq.5).
The following are some general comments on the form of the linearisation coefficients, beginning with the dynamic force terms 
and 
. How these are calculated for a point on the structure depends on whether the seastate is modelled as a regular wave or random sea. In a regular wave analysis the coefficients at a particular location are a function of the amplitude of the relative fluid/structure velocity at that point (Hamilton, 1980). Since this is a function of the (unknown) structure response, an iterative solution is required. For the first iteration the relative velocity is assumed equal to the water particle velocity, and a first estimate of the linearisation coefficients is calculated on this basis. Mathematical Background (Eq.9) is assembled and solved, and relative velocity and linearisation coefficients are updated based on this solution. The analysis proceeds in this way until the change in dynamic response from iteration to iteration is below a certain tolerance.
In a random sea analysis the coefficients are a function of the standard deviation of relative velocity (Langley, 1984), which is calculated by summing over all of the solution harmonic components. Again an iterative procedure is required, with the iteration loop in this case requiring a “sweep” over all the frequencies. The standard deviation of relative velocity and the dynamic drag linearisation coefficients are updated at the end of each sweep, and iteration continues until the change in relative velocity statistics from successive sweeps is less than a certain tolerance.
Turning now to the static force terms 
and 
, it was mentioned earlier that these terms are functions of the dynamic response, and this is true in the case of both regular wave with current and random sea with current. So in both cases the so-called full static solution takes place after the completion of the (iterative) dynamic phase. The full static solution is again iterative, though not because the linearisation coefficients vary with the static solution (they do not), but because the static phase is nonlinear, as previously discussed.