Morison’s Equation represents a semi-empirical approach to hydrodynamics which is commonly used in marine engineering. It assumes that the force exerted by unbroken waves on a cylinder can be represented by a linear sum of drag and inertial terms. Morison’s equation is widely established for modelling wave forces on slender offshore structures such as mooring lines. In situations where the body size becomes significant with respect to wavelength, the underlying assumptions become invalid, and the effects of radiation and diffraction must also be considered. Hence it is generally unsuitable for modelling arbitrary floating bodies. Refer to Diffraction-Radiation Theory & Morison's Equation for a discussion about the main differences between these hydrodynamic modelling approaches.
The velocity potential is classically decomposed into incident, diffraction and radiated potentials. Incident potential represents the wave excitation, diffraction represents disturbance of the wave induced fluid motion due to the presence of a fixed body, while the radiated potential represents the fluid motion caused by a moving body in still water. Radiation-diffraction programs solve the radiation and diffraction potentials, and provide coefficient terms, such as Added Mass, Radiation Damping and Force RAOs, at a range of discrete frequencies which may be readily inserted into Flexcom.
The general equation of motion for a floating structure in six degrees of freedom may be stated as follows:
![]() (1)
(1)
where:
•xj is the displacement in the jth degree of freedom
•Fk(t) is the dynamic external force in the kth degree of freedom
•M is the inertia matrix
•a is the added inertia matrix (frequency dependent)
•C is the system damping matrix (frequency dependent)
•K is the hydrostatic stiffness matrix
A particular consideration arises in relation to the added mass and damping terms, and how these are treated in the time domain. In general these are not constant and vary as a function of frequency of response of the floating body. To deal with this problem Flexcom uses the technique put forward by Cummins (1962). In particular, the frequency dependant damping term is replaced by a convolution integral in the time domain, and the frequency dependent added mass is replaced with a constant value. Thus Equation (1) above is transformed to:
![]() (2)
(2)
Here the frequency independent added inertia coefficients (mkj) and the retardation functions (Rkj) can be computed from:
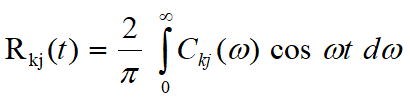 (3)
(3)
 (4)
(4)
The retardation functions are derived from the user-specified frequency dependant damping values and the coefficients of added inertia are derived from the user-specified added mass at a particular frequency (i.e. the reference frequency, ω’).
Once the system of coupled differential equations is obtained, arbitrarily time-varying loads such as wave induced loads, current forces, non-potential fluid reaction forces and non-linear mooring forces may be incorporated as external force contributions. The final equation of motion to be solved is:
 (5)
(5)
If your simulation contains a single regular wave only, the wave excitation occurs at a single frequency, so Flexcom does not typically compute the damping forces using a convolution integral of velocity time history and retardation functions. Instead it uses a constant 6x6 radiation damping matrix, either by selecting one directly from the frequency-dependent radiation damping data, or via interpolation if no data is available at that particular frequency. Should you prefer to use the convolution integral for some reason, perhaps to further investigate software behaviour, you can explicitly request that the convolution be adopted. Refer to *WAVE-GENERAL for further details. Note however that use of the convolution integral in such circumstances is unnecessary and less computationally efficient. Both approaches will produce very similar results, and while there may be some discrepancies in the early stages due to initial transience, results should be consistent once the simulation has reached steady-state.
A number of issues are immediately apparent with respect to the evaluation of R(t). The user can supply a low frequency cut off value, below which C is assumed to be zero everywhere. The user also needs to supply an upper limit on time, above which R(t) should be very small in comparison to R(t=0). If a time limit is not specified, it defaults to 100s (or the total simulation time, if this is less than 100s). A time step also needs to be specified, (typically this will be in the range 0.05 to 0.1) so as the convolution integral in Equation (2) can be evaluated using the trapezoidal rule at each time step.
This leads directly to a critical issue. Equation (2) will be solved at each time step over the total simulation time period. As the convolution integral will have to be re-evaluated at each time step this will mean the solution time will increase in proportion to the square of the simulation time length. After the solution time has passed the maximum time used to define R(t), the total time needed to solve Equation (2) will increase at a constant rate.
With these issues in mind it is advisable that the time step used to define the complete curve for R(t) (in Equation (3) is an integer multiple of the time step used in the solution of Equation (2). If this is not the case it will be necessary at each time increment in the solution to interpolate the curve of R(t) so as the convolution integral can be evaluated. Further, it is therefore not recommended that variable time stepping be used when complex models of floating bodies are analysed.
Flexcom provides a facility whereby the computed retardation functions may be examined and verified by the user. Specifically, the computed functions are echoed to an ACSII file, entitled ‘Ret_Fn_I.dat’, where I is an integer value indicating the number of the relevant floating body. The layout of the output file is as follows:
Time, R11, …, R22, …, R33, …, R44, …, R55, …, R66
where:
•Time is the time value in seconds
•R11 is the heave retardation function value
•R22 is the surge retardation function value
•R33 is the sway retardation function value
•R44 is the yaw retardation function value
•R55 is the roll retardation function value
•R66 is the pitch retardation function value
and the intermediate terms (e.g. R12, R13, R23 etc.) represent the coupled retardation function terms between various degrees of freedom at the relevant time.
•*FLOATING BODY is used to define a floating body and its associated properties.
•*ADDED MASS is used to define added mass for a floating body.
•*RADIATION DAMPING is used to define radiation damping for a floating body.
•*FORCE RAO is used to specify force RAOs for a floating body.
•*WIND is used to specify wind loading.
•*WIND COEFF is used to specify wind coefficients used to determine the wind loading on a floating body or moored vessel.
•*CURRENT COEFF is used to specify current coefficients used to determine the current loading on a floating body or moored vessel.
•*QTF is used to specify Quadratic Transfer Functions (QTFs) that allow the slow drift loads on a floating body or moored vessel to be determined.
•*QTF CALIBRATION FB is used to specify calibration coefficients used to scale the QTF coefficients for a floating body.
•*VISCOUS DRAG is used to define viscous drag for a floating body.
•*HYDRODYNAMIC COUPLING is used to define hydrodynamic coupling between adjacent floating bodies.
•*WAVE-GENERAL is used to specify miscellaneous parameters to wave loading.
If you would like to see an example of how these keywords are used in practice, refer to E02 - CALM Buoy - Complex.