Buoyancy forces effectively represent the resultant of the sum of all the pressure forces acting on a particular element.
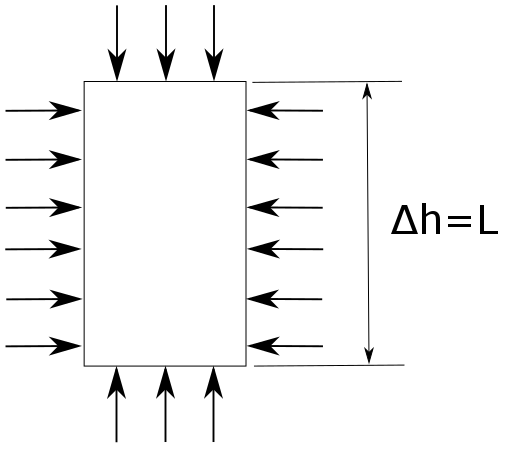
Vertical Element
In the simple case of a vertical element, the pressure forces acting around the element circumference cancel each other out so there is no net horizontal force.
The hydrostatic pressure forces acting on the element faces produce a net vertical force as follows.
![]() (1)
(1)
where:
•FB is the net buoyancy force
•ρ is the density of the ambient fluid (typically seawater)
•g is the acceleration due to gravity
•A is the external cross-sectional area of the element (based on the effective buoyancy diameter)
•Δh represents the change in hydrostatic head (which is equal to the element length in this case)
For a marine structure such a drilling riser, the external cross-sectional area of adjacent elements may be consistent along the riser length, leading to large/concentrated forces at changes in riser cross-section. This point is further elaborated in Buoyancy Formulations.
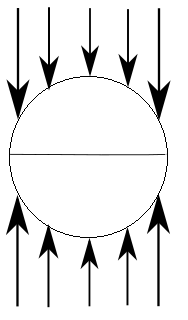
Horizontal Element
In the case of a horizontally aligned element, the pressure forces acting on the element faces cancel each other out so there is no net horizontal force. The pressure forces acting around the element circumference naturally produce a buoyancy uplift, and while the theoretical derivation of the buoyancy force is more complex that the vertical element case, the fundamental principles of pressure differential are equally valid. Specifically, the total buoyancy force may be found by integrating the pressure differential around the element circumference. Theoretically the net buoyancy force caused by hydrostatic pressure may be shown to correspond exactly to the volume of displaced fluid, and this is the modelling approach adopted by Flexcom.
So whether an element is vertical, horizontal, or inclined, the net buoyancy per unit length due to hydrostatic pressure is:
![]() (2)
(2)
This term appears of the right hand side of the Finite Element Equations of Motion. Flexcom evaluates buoyancy forces on an integration point basis, before ultimately transferring the terms to element end nodes.
The presence of waves causes dynamic pressure fluctuations resulting in changes to buoyancy forces. Wave-induced pressure variations reduce with depth below the mean water line so that in deep water the hydrostatic pressure accounts for practically all the uplift force. Closer to the mean water line, dynamic pressure effects can be significant, and are computed as follows:
General water depth (3) |
Deep water (4) |
|
|
where:
•PDyn is the instantaneous dynamic pressure at the point of interest
•H is the wave amplitude
•d is the water depth
•z is the vertical distance below the MWL of the point of interest (e.g. an element integration point)
•θ(t) is the instantaneous wave phase angle at the horizontal location of the point of interest
and the other symbols are as defined previously.
In the case of a single element, the dynamic pressure at the lower end face acts upwards, while the pressure at the upper end face acts downwards. In the case of a vertical series of elements, dynamic pressure forces at adjoining element end faces cancel each other out, leaving just the exposed lower and upper faces, so the situation is the same as for a single element. The net buoyancy force per unit length due to hydrodynamic pressure is:
![]() (5)
(5)
The total buoyancy force is then the sum of the static and dynamic components.
Note: The dynamic component of buoyancy force was not automatically included in versions prior to Flexcom 2024.1. If you are using an older version, it activated manually by setting DYNAMIC PRESSURE=INCLUDE under *HYDRODYNAMIC SETS.