Stokes V Wave Theory |
 
|
Stokes V Wave Theory |
|
The following equations define the wave height 
and the wave celerity 
for a Stokes V regular wave (Chakrabarti, 1987)
(1)
and
(2)
where:
•
is the celerity given by linear wave theory
•
is an unknown along with the wave number 
and the quantities 
and 
are functions only of 
and are listed in 'Stokes V Coefficients' table below. Note that in these expressions 
and 
, where 
represents water depth.
For a given (user-specified) value of 
, the quantities 
and 
are determined from Equations (1) and (2) through an iterative Newton-Raphson technique. Once they have been found, the water surface elevation is found from the following:
where:
Again the relevant 
quantities are listed in the 'Stokes V Coefficients' table below.
The fifth-order velocity potential 
is written in a series form as:
(4)
where the non-dimensional coefficients 
are given by:
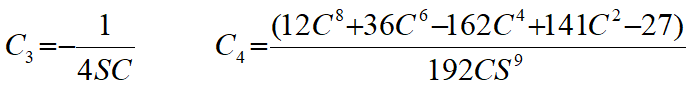(5)
Expressions for the water particle velocities and accelerations are obtained in the usual way by differentiating 
. For example, the vertical water particle velocity is given by:
The complete expressions for 
, 
, 
, and 
are available in standard texts such as Chakrabarti (1987), and are omitted here.
Stokes V Coefficients
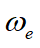
