<< Click to Display Table of Contents >> Navigation:  Flexcom > Theory > Applied Loading > Wave Loading > Advanced Topics >
Water Surface Elevation

This section discusses how the water surface elevation is found at any point in the wave field.

As described in Spectrum Discretisation, a random sea is discretised into component harmonics. The output from this process is essentially a series of regular waves, each with its individual period, amplitude and phase. For a multi-directional random sea, the resulting water surface elevation at a point in the wave field is found as a superposition of these wave components over all wave directions and is given by the equation:

where:

• is the wave amplitude in mth direction of nth harmonic

• is the wave number of nth harmonic

• is the horizontal distance in mth direction from vertical axis Y=Z=0 to point in question

• is the angle of mth wave direction measured anticlockwise relative to global Y

• is the random phase for mth wave direction and nth harmonic

• is the number of harmonics

• is the number of wave directions

For a uni-directional random sea, obviously , and the above Equation becomes:

For a uni-directional random sea, the coefficients are found from the wave spectrum using the relation:

where:

 

The product  is an increment of the area under the spectrum centred on , as shown in the below figure.

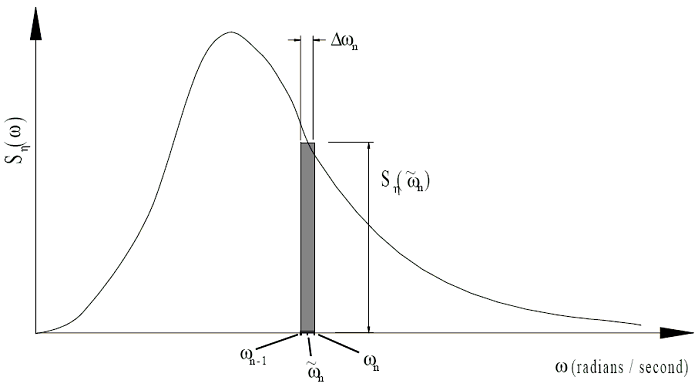
Spectrum Area Increment

The wave amplitudes for a multi-directional random sea are related to the uni-directional values as follows:

where:

• a spreading function used to distribute wave energy about the dominant direction, as described earlier in the ‘Wave Energy Spreading’ section.

• is the mth wave direction relative to dominant wave direction

• is the direction relative to dominant wave direction