When specifying approximate nodal locations, Flexcom requires only that you satisfy two common sense conditions, which can be simply expressed as follows. Firstly, the distance between cable end nodes must not be greater than the length of the cable joining them - the alternative is physically impossible. Secondly, if one of the cable end nodes is on the seabed, the sum of the vertical and horizontal distances between cable end nodes must be greater than the cable length (otherwise the cable profile cannot be found using the catenary equations). These conditions are illustrated schematically below.
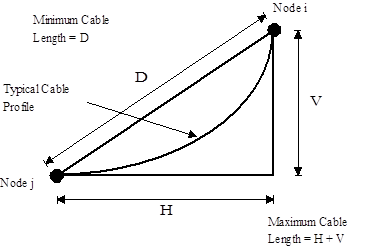
Maximum and Minimum Lengths for Given Nodes
Here the conditions are illustrated in slightly reverse order, by showing the maximum (if Node j is on the seabed) and minimum cable lengths possible for a given nodal separation. It is important to understand that when you calculate approximate locations it is not necessary for program convergence that they are close to the eventual positions. As long as the above conditions are satisfied, the program should converge quickly to the correct locations.
Why the actual coordinates specified for the cable start and end nodes generally represent only approximate locations is again best illustrated by means of an example – consider the case of a steep wave flexible riser illustrated schematically below.
Steep Wave Riser
In defining this system in terms of cables, you would normally use three cables, the first for the lower catenary section from the seabed connection to the start of the buoyant section, the second to represent the buoyant section, and the third for the upper catenary, from the end of the buoyant section to the vessel connection point. To define these three cables, you would need to first define four nodes, at the seabed and vessel connection points, and at the changeover between the buoyant section and the lower and upper catenaries respectively. The coordinates of the two connection points will, of course, be known in advance. Not so the coordinates of the changeover points, because again these locations are part of the solution and will change if the various cable lengths and properties change. How then to define nodal coordinates for these points? The answer is that Flexcom requires only approximate locations for these nodes that satisfy the common-sense conditions described above.
Focusing on the steep wave riser example, the following illustrates how coordinates for the changeover nodes might be calculated for the following values:
Cable lengths: Lower catenary 80m
Buoyant section 130m
Upper catenary 240m
Coordinates: Seabed (0,0,0)
Vessel (310,120,0)
Since the lower catenary will be nearly vertical in the static offset position, possible values for the coordinates of the lower catenary/buoyant section changeover point might be (77,20,0). For these coordinates, the straight-line distance between ends is 77.13m (less than 80m), and the sum of the horizontal and vertical separations is 97m (greater than 80m). So both criteria are satisfied, and (77,20,0) represents an acceptable approximation. For the upper changeover point, possible coordinates might be (110,70,0) – you might want to prove to yourself that these are again acceptable values.
Although it might appear that calculating approximate coordinates in this way requires some ingenuity, in general acceptable values can usually be quickly found from simple geometrical considerations. Finally, it is worth commenting again that where coordinates are approximate, it is not necessary for program convergence that the values specified be close to the eventual correct values (which, of course, are unknown). As long as the approximate coordinates are physically reasonable, the program will converge quickly to the correct solution.