Energy Residual Convergence |
 
|
Energy Residual Convergence |
|
An alternative convergence criteria based on energy residuals is also provided, similar to that proposed by Bathe (1982). This approach may be useful for certain applications – for example in modelling post-buckling responses. In such circumstances, the standard convergence measure described above may not be sufficiently stringent, as it is largely displacement driven. Specifically, while the overall displacement measure may have been satisfied for an entire model at a given iteration, significant variations may still be occurring in localised areas. The energy residual convergence is checked for each degree of freedom using the following formula:
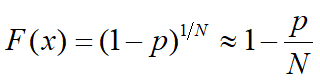
(1)
where:
•
is the increment in displacement between two successive iterations, i and i-1
•
is the displacement at iteration i
•
and 
are the external and internal force terms, respectively, at the current iteration i
•
is the energy tolerance
•
is the Euclidian norm of A, defined as 
Note also that:
•
if the respective node does NOT have a boundary condition imposed for that DOF
•
if the respective node has a boundary condition imposed for that DOF
If 
is negligible, then 
.
This additional criterion works alongside the standard convergence criterion. If you do not specify an energy residual tolerance level, the criterion is not checked. A converged solution is achieved when both criteria are satisfied for a particular iteration.
•*TOLERANCE is used to define the analysis convergence tolerance measure and related data.