This example illustrates how you can model an arbitrary contact surface via the User Solver Variables feature. A sphere is used in this example for simplicity but the feature is fully customisable, the use of custom code enables direct modification of the global stiffness matrix and global force vector.
The model consists of a simple horizontal beam which is initially constrained above a spherical contact surface. For visual purposes, a spherical shape is added as an Auxiliary Body, but this does not affect the numerical simulation. During a restart stage, the beam is allowed to fall freely and make contact with the spherical body below it. In order to verify correct model behaviour, results are compared with an analogous model which uses a Cylindrical Guide Surface.

Sphere Contact Model
The positions of the finite element nodes are monitored for contact with the sphere. Once contact occurs, a local stiffness term is applied in a direction which is perpendicular to the sphere at the contact location. A force vector is also computed to account for the initial separation between the node and the contact surface (because Flexcom solves for position rather than displacement). The custom code uses appropriate local to global transformation matrices to convert the local components into the global axis system before augmenting the global constituent terms. The custom code is effectively replicating (a simplified version of) Flexcom's guide surface contact modelling algorithm, but using a different geometrical pattern to model the sphere.
The beam slides down along the side of the sphere as expected. Results show close correlation with the analogous cylindrical surface model.
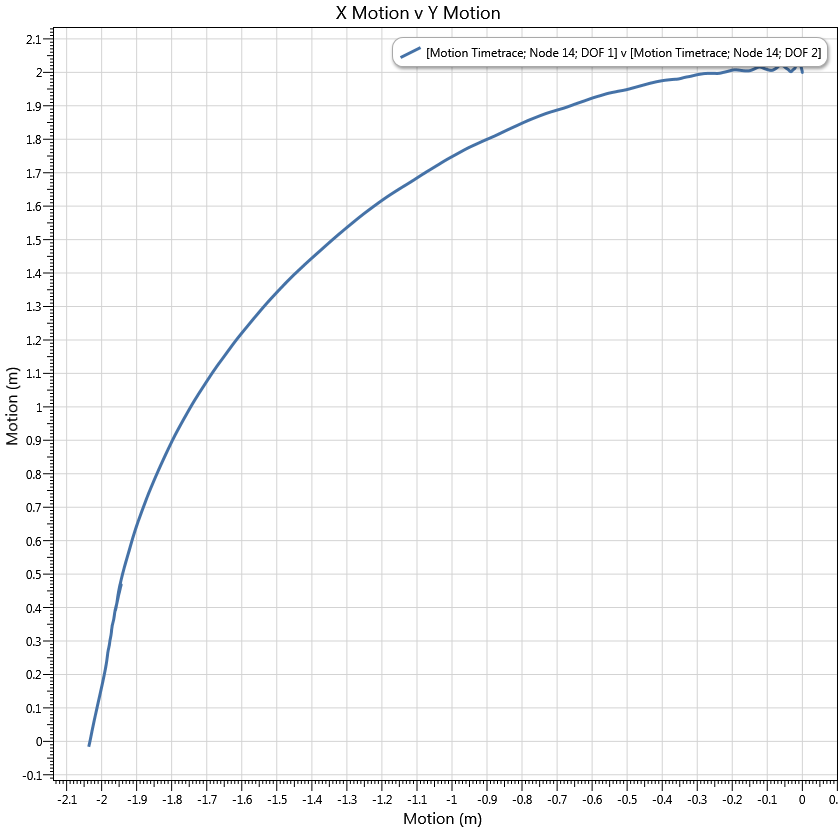
Motion of Beam End Point
Pre-compiled DLLs for both 32-bit and 64-bit operating systems are provided with this example. The original Fortran source code is also provided should you wish to examine it.
subroutine user_solver_variables(iter,time,ramp,nnode,nncon,ncord,nndof,nelmn,necon,nedof, &
size_force,size_mass,size_stiff,elmcon,nodcon,intoun,ietoue,cord,displacement, &
velocity,acceleration,trgb,tglu,disp_prev,pos_prev,vel_prev,acc_prev,axial_force,y_shear, &
z_shear,torque,y_bending,z_bending,eff_tension,y_curvature,z_curvature,force,mass,stiff)
!dec$ attributes dllexport, stdcall, reference :: user_solver_variables
implicit none
! Input variables - cannot be modified within this subroutine
integer, intent(in) :: iter
!dec$ attributes value :: iter
real(8), intent(in) :: time
!dec$ attributes value :: time
real(8), intent(in) :: ramp
!dec$ attributes value :: ramp
integer(4), intent(in) :: nnode
!dec$ attributes value :: nnode
integer(4), intent(in) :: nncon
!dec$ attributes value :: nncon
integer(4), intent(in) :: ncord
!dec$ attributes value :: ncord
integer(4), intent(in) :: nndof
!dec$ attributes value :: nndof
integer(4), intent(in) :: nelmn
!dec$ attributes value :: nelmn
integer(4), intent(in) :: necon
!dec$ attributes value :: necon
integer(4), intent(in) :: nedof
!dec$ attributes value :: nedof
integer(4), intent(in) :: size_force
!dec$ attributes value :: size_force
integer(4), intent(in) :: size_mass
!dec$ attributes value :: size_mass
integer(4), intent(in) :: size_stiff
!dec$ attributes value :: size_stiff
integer(4), intent(in), dimension(nncon, nelmn) :: elmcon
!dec$ attributes reference :: elmcon
integer(4), intent(in), dimension(necon,nnode) :: nodcon
!dec$ attributes reference :: nodcon
integer(4), intent(in), dimension(nnode) :: intoun
!dec$ attributes reference :: intoun
integer(4), intent(in), dimension(nelmn) :: ietoue
!dec$ attributes reference :: ietoue
real(8), intent(in), dimension(ncord,nnode) :: cord
!dec$ attributes reference :: cord
real(8), intent(in), dimension(nndof,nnode) :: displacement
!dec$ attributes reference :: displacement
real(8), intent(in), dimension(nndof,nnode) :: velocity
!dec$ attributes reference :: velocity
real(8), intent(in), dimension(nndof,nnode) :: acceleration
!dec$ attributes reference :: acceleration
real(8), intent(in), dimension(3,3,nelmn) :: trgb
!dec$ attributes reference :: trgb
real(8), intent(in), dimension(3,3,nelmn) :: tglu
!dec$ attributes reference :: tglu
real(8), intent(in), dimension(nndof,nnode) :: disp_prev
!dec$ attributes reference :: disp_prev
real(8), intent(in), dimension(nndof,nnode) :: pos_prev
!dec$ attributes reference :: pos_prev
real(8), intent(in), dimension(nndof,nnode) :: vel_prev
!dec$ attributes reference :: vel_prev
real(8), intent(in), dimension(nndof,nnode) :: acc_prev
!dec$ attributes reference :: acc_prev
real(8), intent(in), dimension(nelmn,3) :: axial_force
!dec$ attributes reference :: axial_force
real(8), intent(in), dimension(nelmn,3) :: y_shear
!dec$ attributes reference :: y_shear
real(8), intent(in), dimension(nelmn,3) :: z_shear
!dec$ attributes reference :: z_shear
real(8), intent(in), dimension(nelmn,3) :: torque
!dec$ attributes reference :: torque
real(8), intent(in), dimension(nelmn,3) :: y_bending
!dec$ attributes reference :: y_bending
real(8), intent(in), dimension(nelmn,3) :: z_bending
!dec$ attributes reference :: z_bending
real(8), intent(in), dimension(nelmn,3) :: eff_tension
!dec$ attributes reference :: eff_tension
real(8), intent(in), dimension(nelmn,3) :: y_curvature
!dec$ attributes reference :: y_curvature
real(8), intent(in), dimension(nelmn,3) :: z_curvature
!dec$ attributes reference :: z_curvature
! Output variables - can be modified within this subroutine if required
real(8), intent(inout), dimension(size_force,nedof) :: force
!dec$ attributes reference :: force
real(8), intent(inout), dimension(nedof,nedof,size_mass) :: mass
!dec$ attributes reference :: mass
real(8), intent(inout), dimension(nedof,nedof,size_stiff) :: stiff
!dec$ attributes reference :: stiff
! Variable names
! iter : Current iteration
! time : Current timestep
! ramp : Ramp
! nnode : Number of nodes in the model
! nncon : Number of nodes with connected elements
! ncord : Number of coordinates
! nndof : Number of degrees of freedom per node (6)
! nelmn : Number of elements in the model
! necon : Number of elements connected
! nedof : Number of degrees of freedom per element (14)
! size_force : Dimension of the global force vector
! size_mass : Dimension of the global mass matrix
! size_stiff : Dimension of the global stiffness matrix
! elmcon : Element connectivity array
! nodcon : Node connectivity array
! intoun : Internal node to user node numbering array
! ietoue : Internal element to user element numbering array
! cord : Initial nodal co-ordinates
! displacement : Nodal displacements at previous iteration
! velocity : Nodal velocities at previous iteration
! acceleration : Nodal accelerations at previous iteration
! trgb : Rigid body rotation (local undeformed -> convected) transformation matrix
! tglu : Global to local undeformed transformation matrix
! disp_prev : Nodal displacements at previous timestep
! pos_prev : Nodal positions at previous timestep
! vel_prev : Nodal velocities at previous timestep
! acc_prev : Nodal accelerations at previous timestep
! axial_force : Axial force in elements at previous timestep
! y_shear : Y Shear forces in elements at previous timestep
! z_shear : Z Shear forces in elements at previous timestep
! torque : Torque in elements at previous timestep
! y_bending : Y bending moments in elements at previous timestep
! z_bending : Z bending moments in elements at previous timestep
! eff_tension : Effective Tension in elements at previous timestep
! y_curvature : Y curvatures in elements at previous timestep
! z_curvature : Z curvatures in elements at previous timestep
! force : Global force vector at previous iteration
! mass : Global mass matrix
! stiff : Global stiffness matrix
! Declare local variables.
integer :: i,j
integer :: int_elem_no
integer :: int_node_no
integer :: local_node
integer :: user_number_of_nodes
integer :: allocate_error
integer :: index
integer, allocatable, dimension(:) :: user_node_no_array
real(8) :: user_sphere_radius
real(8) :: user_sphere_stiffness
real(8) :: distance
real(8) :: penetration
real(8) :: alpha
real(8) :: magnitude_local_unit_vector
real(8) :: pi
real(8) :: dot_prod
real(8) :: orthogonal_magnitude
real(8), dimension(3) :: user_sphere_origin
real(8), dimension(3) :: node_co_ordinates
real(8), dimension(3) :: global_contact_force_array
real(8), dimension(3) :: local_unit_vector
real(8), dimension(3) :: orthogonal_local_unit_vector
real(8), dimension(3) :: position_array
real(8), dimension(3) :: global_co_ordinates_unit_vector
real(8), dimension(3,3) :: rotation_matrix
real(8), dimension(3,3) :: transpose_rotation_matrix
real(8), dimension(3,3) :: local_stiffness_matrix
real(8), dimension(3,3) :: global_stiffness_matrix
real(8), dimension(3,3) :: interm_stiffness_matrix
real(8), dimension(nedof,nedof) :: elem_stiff
logical :: is_node_ok
logical :: start_node
logical :: end_node
! Sphere Contact Test
! User data
user_number_of_nodes = 2
user_sphere_radius = 2.0d0
user_sphere_stiffness = 1.0d3
user_sphere_origin = [0.0d0, 0.0d0, 0.0d0]
! Allocate array of node numbers for which calculations are performed.
do i = 1, 1
allocate(user_node_no_array(user_number_of_nodes), stat=allocate_error )
if( allocate_error /= 0 )exit
user_node_no_array = [1,2]
end do
! Internal works
! Pi
pi = 4.0d0 * datan(1.0d0)
do index = 1, user_number_of_nodes
int_elem_no = 0
int_node_no = 0
local_node = 0
is_node_ok = .false.
start_node = .false.
end_node = .false.
alpha = 0.0d0
distance = 0.0d0
penetration = 0.0d0
orthogonal_magnitude = 0.0d0
dot_prod = 0.0d0
magnitude_local_unit_vector = 0.0d0
node_co_ordinates = 0.0d0
local_unit_vector = 0.0d0
global_co_ordinates_unit_vector = 0.0d0
orthogonal_local_unit_vector = 0.0d0
global_contact_force_array = 0.0d0
local_stiffness_matrix = 0.0d0
interm_stiffness_matrix = 0.0d0
global_stiffness_matrix = 0.0d0
rotation_matrix = 0.0d0
transpose_rotation_matrix = 0.0d0
! Check if user element exists in Flexcom list of elements and set internal element number
! if element exists.
do i = 1,nnode
if( user_node_no_array(index) == intoun(i) )then
int_node_no = i
is_node_ok = .true.
end if
end do
! Start calculations
if( is_node_ok ) then
! Get instantaneous co-ordinates of Local Node
do i = 1,3
node_co_ordinates(i) = cord(i,int_node_no) + displacement(i,int_node_no)
end do
! Distance from origin of the sphere to End Node
distance = norm2( node_co_ordinates - user_sphere_origin )
! Penetration
penetration = user_sphere_radius - distance
! Proceed calculations for value of penetration greater than zero
if ( penetration > 1.0d-10 )then
! Fill in local stiffness matrix
local_stiffness_matrix(1,1) = user_sphere_stiffness
! Unit vector of the local axis system which gives the direction of contact force
local_unit_vector = ( node_co_ordinates - user_sphere_origin ) / ( distance )
! Global co-ordinates vector (global X axis)
global_co_ordinates_unit_vector = [1.0d0, 0.0d0, 0.0d0]
! Vector orthogonal to the global X axis and local_unit_vector
orthogonal_local_unit_vector(1) = global_co_ordinates_unit_vector(2)*local_unit_vector(3) - global_co_ordinates_unit_vector(3)*local_unit_vector(2)
orthogonal_local_unit_vector(2) = global_co_ordinates_unit_vector(3)*local_unit_vector(1) - global_co_ordinates_unit_vector(1)*local_unit_vector(3)
orthogonal_local_unit_vector(3) = global_co_ordinates_unit_vector(1)*local_unit_vector(2) - global_co_ordinates_unit_vector(2)*local_unit_vector(1)
orthogonal_magnitude = norm2( orthogonal_local_unit_vector )
orthogonal_local_unit_vector = orthogonal_local_unit_vector / orthogonal_magnitude
! Magnitude of Local unit vector
magnitude_local_unit_vector = dsqrt( local_unit_vector(1)**2 + local_unit_vector(2)**2 + local_unit_vector(3)**2 )
! Angle between global X axis and local_unit_vector
dot_prod = global_co_ordinates_unit_vector(1)*local_unit_vector(1) + global_co_ordinates_unit_vector(2)*local_unit_vector(2) +global_co_ordinates_unit_vector(3)*local_unit_vector(3)
if ( magnitude_local_unit_vector > 1.0d-10 )then
alpha = dacos( dot_prod / magnitude_local_unit_vector )
else
alpha = 0.0d0
end if
! Normalise angle to interval [-pi,pi]
if( alpha < - pi )then
do while (alpha < - pi)
alpha = alpha + (2.d0 * pi)
end do
else if( alpha > pi )then
do while (alpha > pi)
alpha = alpha - (2.d0 * pi)
end do
end if
! get rotation matrix and transpose of roation matrix
call calculate_rotation_matrix(alpha, orthogonal_local_unit_vector, rotation_matrix, transpose_rotation_matrix)
! Get internal element number
int_elem_no = nodcon(1,int_node_no)
! Set Local Node
if ( int_node_no == elmcon(1,int_elem_no) )then
local_node = 1
else
local_node = 2
end if
! Premultiply local stiffness matrix with transpose of rotation matrix
interm_stiffness_matrix = matmul( transpose_rotation_matrix, local_stiffness_matrix )
! Get global stiffness matrix - postmultiply interm_stiffness_matrix with rotation matrix
global_stiffness_matrix = matmul( interm_stiffness_matrix, rotation_matrix )
! Store element stiffness matrix
elem_stiff(:,:) = 0.0d0
if ( local_node == 1 )then
elem_stiff(1:3,1:3) = global_stiffness_matrix(:,:)
else
elem_stiff(7:9,7:9) = global_stiffness_matrix(:,:)
end if
! Augment the global stiffness matrix
stiff(:,:,int_elem_no) = stiff(:,:,int_elem_no) + elem_stiff(:,:)
! Position array
position_array = [ user_sphere_radius, 0.0d0, 0.0d0]
! Premultiply local position array with transpose of rotation matrix
position_array = matmul(transpose_rotation_matrix,position_array) + user_sphere_origin
! Get global nodal load
global_contact_force_array = matmul(global_stiffness_matrix,position_array)
! Augment the force with global contact force.
! DOF 1-3 for Start Node, DOF 7-9 for End Node
if ( local_node == 1 )then
force(int_elem_no,1:3) = force(int_elem_no,1:3) + global_contact_force_array(:)
else
force(int_elem_no,7:9) = force(int_elem_no,7:9) + global_contact_force_array(:)
end if
end if
end if
end do
! Deallocate array
if(allocated(user_node_no_array)) deallocate(user_node_no_array)
! Do not alter the next line.
end subroutine user_solver_variables
! ***************************************************************************************
! ***************************************************************************************
! ***************************************************************************************
! ***************************************************************************************
! Subroutine to calculate rotation matrix for an array rotated by an angle alpha about
! an axis defined by an orthogonal_local_unit_vector. Transpose of the rotation matrix is
! calculated as well.
subroutine calculate_rotation_matrix(angle, vector, rotation_matrix, transpose_rotation_matrix)
implicit none
! Declare arguments
real(8), intent(in) :: angle
real(8), intent(in), dimension(3) :: vector
real(8), intent(inout), dimension(3,3) :: rotation_matrix
real(8), intent(inout), dimension(3,3) :: transpose_rotation_matrix
! Rotation matrix
rotation_matrix(1,1) = dcos(angle) + vector(1) * vector(1) * ( 1 - dcos(angle) )
rotation_matrix(2,1) = vector(1) * vector(2) * ( 1 - dcos(angle) ) - vector(3) * dsin(angle)
rotation_matrix(3,1) = vector(1) * vector(3) * ( 1 - dcos(angle) ) + vector(2) * dsin(angle)
rotation_matrix(1,2) = vector(2) * vector(1) * ( 1 - dcos(angle) ) + vector(3) * dsin(angle)
rotation_matrix(2,2) = dcos(angle) + vector(2)* vector(2) * ( 1 - dcos(angle) )
rotation_matrix(3,2) = vector(2) * vector(3) * ( 1 - dcos(angle) ) - vector(1) * dsin(angle)
rotation_matrix(1,3) = vector(3) * vector(1) * ( 1 - dcos(angle) ) - vector(2) * dsin(angle)
rotation_matrix(2,3) = vector(3) * vector(2) * ( 1 - dcos(angle) ) + vector(1) * dsin(angle)
rotation_matrix(3,3) = dcos(angle) + vector(3)* vector(3) * ( 1 - dcos(angle) )
! Transpose rotation matrix
transpose_rotation_matrix = transpose(rotation_matrix)
end subroutine calculate_rotation_matrix
Source Code