Deans Stream Theory |
 
|
Deans Stream Theory |
|
Fourier series wave theory derives its name from an approximate solution to the governing wave equation using a Fourier cosine series in θ, as follows:
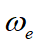(1)
where:
•ψ is the Stream Function
•
is the mean value of horizontal fluid velocity for a constant value of x, over one wavelength
•d is the water depth
•x is the height above the mean water line
•g is the acceleration due to gravity
•k is the wave number
•Bj is a set of dimensionless Fourier coefficients
•N is the order of the stream function. This is a measure of how non-linear the wave is. In deep water the order can be relatively low (between 3 and 5), while in very shallow water the order can be as high as 30.
This formulation for the stream function, combined with the dynamic and kinematic free surface boundary conditions and the dispersion relationship are used to set up a system of complex non-linear equations. The unknown variables in the stream function equation can then be calculated for any given set of wave height, wave period, water depth and underlying current velocity. The wave kinematics (surface elevation, water particle velocities and accelerations etc.) are then derived from the solution of the governing equation.
The water surface elevation at any point in the wave field is found using the following equation:
where:
and:
•θ = ks - wt
•s is the horizontal distance from vertical axis Y=Z=0 to point in question (s = ycosϕ + zsinϕ)
•y is the horizontal distance from vertical axis to point in global Y direction
•z is the horizontal distance from vertical axis to point in global Z direction
The wave spacial origin can be specified via the *WAVE-GENERAL keyword such that s becomes 
where ŷ & ẑ are the specified y and z offsets from the origin.
•ϕ is the wave direction relative to global Y
•w is the wave circular frequency (w = 2π/T)
•T is the wave period
•t is the present solution time
