A multi-directional random sea is defined in terms of a dominant wave direction and the number of wave directions. The dominant wave direction is the direction at which most of the wave energy is concentrated. A definition of the dominant wave direction, denoted θdom is shown in the first figure below. If the number of specified directions is denoted n, then Flexcom divides a semi-circular arc between (θdom- 90°) and (θdom+ 90°) into n equal segments, as shown for example in the second figure below, where 3 wave directions are specified. The vector centred on the origin and bisecting the segment defines a wave direction corresponding to each segment. Note that if the number of wave directions is even, this process will not result in a wave direction coincident with the dominant, so an odd value is recommended.
Flexcom uses a cosinen spreading function in distributing wave energy between directions in a multi-directional random sea, where n is a user-defined wave spreading exponent. The spreading exponent must be an even integer and defaults to 2, giving a cosine2 spreading function.

Dominant Wave Direction
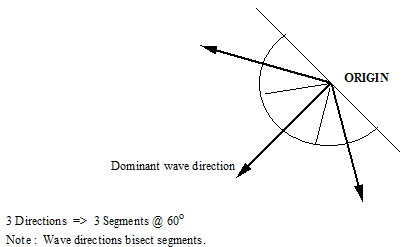
Wave Spreading Directions
A mathematical description of a directional seastate is feasible by assuming that the sea state can be considered as a superposition of a large number of regular sinusoidal wave components with different frequencies and directions. With this assumption, the representation of a spectrum in frequency and direction becomes a direct extension of the frequency spectrum alone, allowing the use of Fast Fourier Transform method. It is often convenient to express the wave spectrumE(f,θ) describing the angular distribution of wave energy at respective frequencies by:
![]()
where the function G(f,θ) is a dimensionless quantity, and is known as the directional spreading function. Other acronyms for G(f,θ) are the spreading function, angular distribution function and the directional distribution.
The one-dimensional spectra may be obtained by integrating the associated directional spectra over θ as:
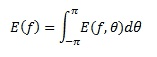
Therefore, from the above last two equations, G(f,θ) must satisfy:

The functional form of G(f,θ) has no universal shape and several proposed formulas are available.
In the most convenient simplification of G(f,θ), it is customary to consider G to be independent of frequency f, such that we have:

The above can be generalised to:
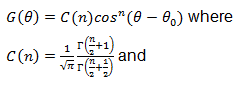
•θ0 is the dominant (principal) direction for the spectrum
•n is the wave spreading exponent that determines the peakedness of the directional spreading
•C(n) is a constant satisfying the normalization condition
•θ is a counterclockwise measured angle from the principal wave direction
•Γ is the Gamma function
If you plot the G function with respect to the angle, you will look at a bell graph. The peak and mean of this bell graph will be at the dominant direction.
The standard referring the wave spreading exponent is DNV RP-C205-2010 - environmental conditions and loads. This is recommended practice only, the formulation above is purely mathematical.
Variations in wave spreading exponent
If you increase the spreading exponent then you are focusing most of the energy around the dominant direction and less towards the peripheral directions. In Flexcom, the directional spreading function G does not depend on frequency f. As a result, after the discretisation of the specified spectrum, the amplitude of each harmonic is scaled with the G function based on the angle. The scaling is repeated for each wave direction you requested. So, if a spectrum is discretised with 100 harmonics and you requested 3 directions you should get 300 harmonics in your load case.
Wave spectra may be defined using any of the following keywords:
•*WAVE-PIERSON-MOSKOWITZ is used to specify a Pierson-Moskowitz random sea wave spectrum or spectra.
•*WAVE-JONSWAP is used to specify a JONSWAP random sea wave spectrum or spectra.
•*WAVE-OCHI-HUBBLE is used to specify an Ochi-Hubble random sea wave spectrum or spectra.
•*WAVE-TORSETHAUGEN is used to specify a Torsethaugen random sea wave spectrum or spectra.
•*WAVE-TIME-HISTORY is used to specify a random seastate in terms of a time history of water surface elevation.
•*WAVE-USER-DEFINED is used to specify a User-Defined random sea wave spectrum or spectra.
Each keyword has an associated Wave Spreading Exponent input, which defines the exponent used in distributing wave energy between directions in a multi-directional random sea.