The timetrace of a structural response does not always follow a Gaussian distribution. In these cases the individual maxima in the timetrace can be Weibull distributed. The Weibull cumulative distribution is defined as:
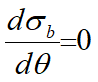 (1)
(1)
where a, b and c are known as the location, scale and shape parameters, respectively. The maxima are measured as amplitudes above the mean. The method of determining these parameters is described further below. The Rayleigh distribution is a special case of Weibull with a = 0, b = (2m0)0.5 and c = 2. The values of a, b and c will often be close to the Rayleigh values.
The estimate of the extreme value is determined from the previous Equations and Equation (1) above as:
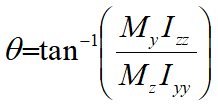 (2)
(2)
The number of individual maxima in a timetrace N is determined as per Rayleigh (Eq.4). Note, however, that the extreme minima are obtained from first negating the timetrace as previously described above and performing a separate Weibull fit of the data.
The parameters of the Weibull distribution are determined by a standard procedure of transforming Equation (1) to a straight-line relationship and performing a least-squares fit of the slope and intercept. The straight line is defined by:
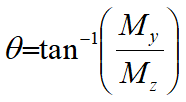 (3)
(3)
where M and D denote the slope and Y-axis intercept. The data values for X and Y are defined:
![]() (4)
(4)
where k = 1, …, n_count, x(k) denotes the individual maxima in the timetrace sorted in ascending order and F(k) is estimated using the plotting position:
![]() (5)
(5)
A threshold option is also available for the least-squares fit of the Weibull distribution. The threshold removes (censors) smaller maxima from the least-squares fit so that better accuracy can be obtained in fitting the tail of the Weibull distribution. The above procedure is modified by restricting k = kT , …, n_count where kT denotes the threshold value of k. The threshold parameter is specified as a value greater than 0 and less than or equal to 1. A threshold of 1 accepts all the maxima in the least-squares fit. A threshold of 1/3 accepts the upper 1/3 of largest maxima. A direct comparison of the Rayleigh and Weibull fits requires the threshold is equal to 1. The alternative 1/3 value is analogous to the significant wave, which is based on the 1/3 highest waves. Other threshold values can also be chosen.
•*STATISTICS is used to request the creation of statistics plots.
•*EXTREMA is used to specify the procedure and input parameters to be used in the computation of extreme values.