<< Click to Display Table of Contents >> Navigation:  Flexcom > Theory > Model Building > Geometric Properties > Geometric Properties in Flexible Riser Format >
Mass and Polar Inertia per Unit Length

Mass and Polar Inertia

The mass per unit length and the polar inertia per unit length are related terms. The mass per unit length is a measure of the inertia of the structure with respect to translation. The polar inertia is a measure of the inertia of the structure with respect to torsional rotations about the cross section axis.

The mass per unit length m is calculated as the product of the cross-sectional area A and the mass density (mass per unit volume) r of the material. Similarly the polar inertia per unit length p is the product of the polar moment J of the cross-section and the mass density r. The dimensions of p are [Mass][Length]. In the SI system of units, p is typically in kg.m. In Imperial units, p is typically in slugs.ft.

Note that the influence of the value of p on the solution in very many cases is small. Also, in a 2D analysis, the value of p (and indeed the value of GJ) is of course immaterial.

Example Polar Inertia Calculation

Consider a steel pipe as shown in the figure below. The density of the pipe material is 7850 kg/m3. The pipe inside and outside diameters are 0.30m and 0.35m respectively. The calculation of p is as follows:

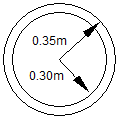
Example Polar Inertia Calculation

Polar moment, J, is given by:

 = 6.78´10-4 m4

Polar moment of inertia per unit length, p = J.

 = (6.78´10-4).(7850) kg.m

 = 5.32 kg.m