Stress Ranges |
 
|
Stress Ranges |
|
The various quantities required to complete the fatigue analysis can be evaluated from the calculated hot spot stress spectrum, or more correctly from the moments of the stress spectrum about the origin, which are defined as:
where mn denotes the nth spectral moment and the remaining symbols are as described previously.
In order to complete the analysis using these moments, certain assumptions are made regarding the distribution of stress peaks and ranges. The first assumption concerns the probability distribution function (pdf) that can be used to determine the probability of occurrence of various stress peaks. You can choose between either the Rayleigh distribution or Dirlik’s rainflow range distribution. The Rayleigh distribution is completely defined by m0, the zeroth moment or the area under the stress spectrum curve. This distribution is suitable for stress spectra that are narrow banded. The Dirlik distribution is defined by m0, m1, m2, and m4, the zeroth, first, second, and fourth moments of the stress spectrum. This distribution is more appropriate when stress spectra are broad banded. Since either distribution refers to stress peaks and in fatigue analysis stress ranges are of interest, the further assumption must also be made that each peak magnitude is half the magnitude of the corresponding stress range. The probability of occurrence of various stress ranges in the response to a particular seastate can therefore be calculated by dividing the area under the corresponding probability distribution curve into a finite number of areas.
In the case of the RAOs mode of operation, the total number of all stress peaks (and hence stress ranges) in one year for a particular seastate i, for a particular direction j, denoted Mij, can be calculated from m0, m2 and m4, the zeroth, second and fourth moments of the stress response spectrum respectively, as follows:
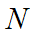(2)
In the case of the Stress Spectra mode of operation, LifeFrequency is dealing directly with the stress spectra produced by these runs, so there is no need for the fatigue program to know the actual combinations of environmental conditions corresponding to each run. The only environmental data required is the percentage annual occurrence of this combination. The percentage value you input in this case is used in a slightly amended form of the Equation above, where it replaces the product “(% occurrence of seastate i) * (% occurrence of direction j)”. The amended form of the equation is:
(3)
Tzs is the mean stress up-crossing period, is given by:
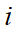(4)
The probability of occurrence of a particular stress range Sk in the response to seastate i and direction j, denoted pij(Sk), is evaluated by integrating the area under the distribution curve between appropriate ordinates, thus:
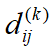(5)
where p(x) is the probability distribution, and 
is chosen on the basis of a suitable subdivision of the area under the curve into a finite number of areas. The Rayleigh distribution is given by:
(6)
The Dirlik distribution is given by:
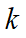(7)
where:
|
|
|
|
|
|
|
|
|
|
The actual number of occurrences in one year of stress range Sk in response to seastate i, direction j, denoted nij (Sk), or simply nijk, is given by:
(18)
•*PDF is used to specify the probability density function to be used in calculating fatigue life estimates from stress spectra.
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)