The hydrodynamic loads on the vessel, denoted ![]() ,
, ![]() and
and ![]() , are determined according to the theory of manoeuvrability as follows:
, are determined according to the theory of manoeuvrability as follows:
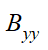 (1)
(1)
where:
•![]() is the vessel added mass in surge
is the vessel added mass in surge
•![]() is the vessel added mass in sway
is the vessel added mass in sway
•![]() is the vessel added mass in yaw
is the vessel added mass in yaw
•![]() is the vessel added mass in sway-yaw coupling
is the vessel added mass in sway-yaw coupling
•![]() is the instantaneous vessel orientation as defined in Local Vessel Axis System figure
is the instantaneous vessel orientation as defined in Local Vessel Axis System figure
•![]() and
and ![]() are the components, in the vessel axis system, of the relative vessel/current velocity.
are the components, in the vessel axis system, of the relative vessel/current velocity.
![]() and
and ![]() are given by the equations:
are given by the equations:
![]() (2)
(2)
where ![]() and
and ![]() are the components in the vessel axes of the vessel CoG velocity;
are the components in the vessel axes of the vessel CoG velocity; ![]() is the current velocity magnitude (which is a user input); and
is the current velocity magnitude (which is a user input); and ![]() is the current direction as defined in the above figure. Differentiating
is the current direction as defined in the above figure. Differentiating ![]() and
and ![]() with respect to time (assuming a constant current velocity) gives:
with respect to time (assuming a constant current velocity) gives:
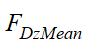 (3)
(3)
Substituting the above expressions into the equations for the hydrodynamic loads gives the following:
 (4)
(4)
For numerical reasons it is desirable to move any terms consisting of the product of a mass by a structure acceleration term to the left-hand side of the overall matrix equations of motion solved by Flexcom. So Term (1) in ![]() , Terms (1) & (4) in
, Terms (1) & (4) in ![]() , and Terms (1) & (2) in
, and Terms (1) & (2) in ![]() are moved in this way. This is achieved by adding the relevant vessel added mass terms to the mass matrix at the location corresponding to the vessel centre of gravity. The following expressions are then used to calculate the hydrodynamic forces which are applied at the vessel CoG:
are moved in this way. This is achieved by adding the relevant vessel added mass terms to the mass matrix at the location corresponding to the vessel centre of gravity. The following expressions are then used to calculate the hydrodynamic forces which are applied at the vessel CoG:
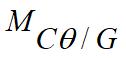 (5)
(5)
•*MOORED VESSEL is used to define a moored vessel and its associated properties. Specifically, the TYPE=MASS inputs are used to specify mass and added mass data.
If you would like to see an example of how this keyword is used in practice, refer to D01 - Moored Vessel.