Gaussian Quadrature |
 
|
Gaussian Quadrature |
|
Exact integration of expressions for element matrices can be difficult, so numerical integration (also referred to as quadrature) is an essential part of finite element analysis. Quadrature is used in numerical analysis, to approximate the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration. Gaussian quadrature is constructed to yield an exact result for polynomials of degree (2n − 1). The domain of integration is [−1, 1], so the integral is written as:
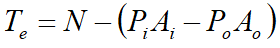(1)
where xi is a designated evaluation point, and wi is the weight of that point in the sum. For the purposes of finite element analysis, the calculations involved in determining the values of 
, the function to be integrated, may be complex. So the Gaussian processes are ideally suited, requiring the least number of such evaluations. The table below summarises the positions and weighting coefficients for Gaussian quadrature.
Gaussian Abscissae and Weight Coefficients
Number of Integration Points |
Location (xi) |
Weight (wi) |
2 |
±0.5773502691 |
1.0 |
3 |
0.0 ±0.7745966692 |
0.888888889 0.555555555 |
5 |
0.0 ±0.5384693101 ±0.9061798459 |
0.568888889 0.478628670 0.236926885 |
10 |
±0.14887434 ±0.43339539 ±0.67940957 ±0.86506337 ±0.97390653 |
0.29552422 0.26926672 0.21908636 0.14945135 0.06667134 |