*Time stepping
To select the time stepping algorithm and to define associated numerical damping coefficients.
Refer to Time Integration Algorithms for further information on this feature.
A block of two lines to select the time stepping algorithm and to specify the numerical damping coefficients. You can specify either Generalised-Alpha (the default) or Hilber-Hughes. There are actually two possible formats for Generalised-Alpha, depending on how you specify the coefficients:
Generalised-Alpha:
TYPE=GENERALISED-ALPHA
P-INFINITY=[P-Infinity]
Or:
TYPE=GENERALISED-ALPHA
[Alpha-f][, Alpha-m]
If you do not specify any coefficients, the program assumes a P-Infinity value of 0.4, and the Alpha-f (0.286) and Alpha-m (-0.143) coefficients are derived from this.
TYPE=HILBER-HUGHES
[Numerical Damping Coefficient]
The Numerical Damping Coefficient defaults to -0.25.
Input: |
Description |
ρ-Infinity: |
The spectral radius at infinity, ρ∞. A value of 0.4 is assumed by default unless you specify otherwise. Experience with Flexcom models have suggested that this is an optimal value which helps to ensure a robust temporal integration model without adversely affecting solution accuracy. Unless specified explicitly, the αf and αm coefficients are derived from ρ∞. |
Alpha-f: |
The numerical damping coefficient αf. |
Alpha-m: |
The numerical damping coefficient αm. |
Input: |
Description |
Hilber Hughes Damping Coefficient: |
The numerical damping coefficient. This defaults to a value of -0.25. Values must be between 0 and –1/3. |
(a)Varying the default values may improve convergence in some highly sensitive analyses, however you should use this keyword very rarely or not at all.
(b)Default values for αf (0.286) and αm (-0.143) for Generalised-Alpha time stepping are derived from ρ∞ as follows:
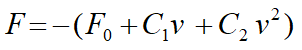
(c)If you specify αf =0.25 and αm=0 for the Generalised-Alpha time stepping algorithm, this effectively replicates the Hilber-Hughes-Taylor operator.
(d)Earlier versions of Flexcom (up to and including Flexcom 8.10) used the Hilber-Hughes-Taylor operator as the default. Generalised-Alpha has since been shown to provide more effective numerical damping, particularly for sensitive models, so it is now the default method. If you are re-running some old simulations which previously used Hilber-Hughes, it is possible that you may notice some very slight differences in results.